Abstract: In this work, the (1–x)Bi0.5Na0.5TiO3–xBaNi0.5Nb0.5O3 (BNT–BNN; 0.00 ≤ x ≤ 0.20) ceramics were prepared via a high-temperature solid-state method. The crystalline structures, photovoltaic effect, and electrical properties of the ceramics were investigated. According to X-ray diffraction, the system shows a single perovskite structure. The samples show the normal ferroelectric loops. With the increase of BNN content, the remnant polarization (Pr) and coercive field (Ec) decrease gradually. The optical band gap of the samples narrows from 3.10 to 2.27 eV. The conductive species of grains and grain boundaries in the ceramics are ascribed to the double ionized oxygen vacancies. The open-circuit voltage (Voc) of ~15.7 V and short-circuit current (Jsc) of ~1450 nA/cm² are obtained in the 0.95BNT–0.05BNN ceramic under 1 sun illumination (AM1.5G, 100 mW/cm²). A larger Voc of 23 V and a higher Jsc of 5500 nA/cm² are achieved at the poling field of 60 kV/cm under the same light conditions. The study shows this system has great application prospects in the photovoltaic field.
Keywords: Bi0.5Na0.5TiO3–BaNi0.5Nb0.5O3; ferroelectric semiconductors; optical band gap; photovoltaic effect; impedance spectroscopy
1 Introduction
Growing energy shortage and deterioration of the environment promote the research and utilization of new energy. Photovoltaic technology and industry have been developed rapidly under the condition of current energy crisis [1–4]. Solar cells based on traditional silicon-based technology are widely used in reality, but the high price of raw materials limits its further development [5]. Fortunately, the ferroelectric photovoltaic (FEPV) effect observed in perovskite materials has aroused great interest of researchers because of its potential in solar cells with good stability and easily available raw materials [6–9]. Much work has been done about the FEPV effect in ferroelectric perovskite oxides, such as BiFeO3 [10,11], BaTiO3[12–15], and Bi0.5Na0.5TiO3 (BNT) compounds [16]. Unfortunately, the bandgaps of most perovskite-oxide ferroelectrics are higher than 3.2 eV. For energy utilization, ferroelectric materials absorbing ultraviolet (UV) rays containing only 3.5% of solar radiation intensity are of little significance [17]. Therefore, an adjustable narrow-band gap is of great significance for improving the photovoltaic effect of ferroelectric materials.
As one of the classic perovskite-oxide ferroelectrics, Bi0.5Na0.5TiO3 (BNT) has attracted considerable attention in the photovoltaic field due to its large spontaneous ferroelectric polarization, high large opto-electrical coefficient, and adjustable band gap [18]. A lot of research have been done by the researchers on the outstanding properties of dielectric [19], piezoelectric [20], and ferroelectric of BNT materials [21]. Unfortunately, there are few of research on the photovoltaic applications based on BNT materials. As an environmentally friendly ferroelectric material, BNT exhibits a high Curie temperature (TC) of ~320 ℃ and large residual polarization (Pr) of ~38 μC/cm² [22]. The large spontaneous polarization of BNT can make it possible for their photovoltaic applications, due to that the light-excited carriers can be effectively separated under the internal bias field formed by spontaneous polarization of ferroelectrics [23–25]. However, the bandgaps of pure BNT is higher than 3.1 eV, and thus the absorption of light is mainly in the deep UV region, which restricts their development in the field of photovoltaics [26].
In recent years, much effort had been done by researchers to optimize the optical characteristics of BNT materials. For example, Bi0.5Na0.5TiO3–NiTiO3 [27], Bi0.5Na0.5TiO3–SrFeO3−δ [28], Bi0.5Na0.5TiO3–SrMnO3−δ[29], and Bi0.5Na0.5TiO3–MgCoO3−δ [30] were successfully prepared by Dang Duc Dung and co-workers. The band gap and ferroelectric properties of BNT can be regulated by substitution at the A/B sites of perovskite oxides. For example, Grinberg et al. [23] first described that the introduction of BaNi0.5Nb0.5O3 could reduce the band gap of pure KNbO3 and produce a higher Jsc of 100 nA/cm².
Based on the above considerations, the BaNi0.5Nb0.5O3-doped Bi0.5Na0.5TiO3 materials were chosen as the research object. In this work, the influence factors (polarization, light intensity) of photocurrent density were studied systematically. Under one sun AM1.5G illumination (100 mW/cm²) and after the polarization, a Jsc of ~5500 nA/cm² for the sample with x = 0.05 is achieved, which is about 55 times larger than that of KBNNO ceramic [23]. Furthermore, the crystal structures and electrical properties of the system were also characterized in detail.
2 Experimental details
The (1–x)Bi0.5Na0.5TiO3–xBaNi0.5Nb0.5O3 (BNT–BNN; 0.00 ≤ x ≤ 0.20) lead-free ceramic samples were synthesized by a solid-state reaction technique. The Na2CO3 (> 99%, Aladdin, China), BaCO3 (> 99.5%, Aladdin, China), NiO (> 98%, Aladdin, China) (> 99.5%, Aladdin, China), Nb2O5 (> 99.9%, Aladdin, China), Bi2O3 (> 99%, Aladdin, China), and TiO2 (> 99%, Aladdin, China) were used as raw materials and milled in anhydrous ethanol medium for 24 h. After that, these mixed powders were dried, sieved, and calcined at 900 ℃ for 12 h. Subsequently, the powders were pressed into pellets with 5 wt% polyvinyl alcohol (PVA) binder under 100 MPa. At last, the pellets were heated at 600 ℃ for 2 h to burn out the PVA binder and calcined at the temperature range 1100–1140 ℃ for 3 h.
The crystalline structure was determined via X-ray diffraction (XRD, PLXCEL 3D, PANALYTICAL, the Netherlands), ranging from 20° to 80°. The surface morphology was observed with scanning electron microscope (FE-SEM, Quanta FEG-450, FEI, USA). Transmission electron microscopy (TEM) images were observed using FEI talosf200s microscopes operating at an accelerating voltage of 200 kV. The lattice vibration modes of the ceramics were recorded by Raman spectra (Horiba Jobin-Yvon Inc., Paris, France). The electric induced polarization loops (P–E) were recorded via a ferroelectric (FE) test equipment (TF Analyzer 2000HS, AACHEN, Germany). The light absorption efficiency of the samples was measured via a UV–Vis–NIR (Lambda 750 s) spectrophotometer. The impedance analyzer (Agilent 4294A, USA) helped to measure the impedance spectroscopy in frequencies (40–106 Hz) and at temperatures (400–650 ℃). In order to test the photovoltaic effect of the sample, a layer of indium tin oxide (ITO) film electrode was sputtered on one side of the ceramic samples and silver was pasted on the other surface. The composite ceramic device has the diameter of 10 mm and thickness of 0.30 mm. The J–V curves of samples under simulated illumination were measured by 2410 light source instrument.
3 Results and discussion
The XRD spectra of (1–x)BNT–xBNN ceramic samples are shown in Fig. 1. These patterns illustrate a pure perovskite structure phase without any trace of secondary phases. The pure BNT ceramic samples are indexed well to the standard JCPDS Card No. 04-011-0431. With the addition of BNN, the (104) and (110) peaks gradually merge, reflecting a change of its structure (rhombohedral to tetragonal structures). A magnification within the 2θ range of 31° to 34° is shown in Fig. 1(b). As the BNN fraction in the solid solutions increases, the (104)/(110) peaks shifted towards lower 2θ angles, ascribed to the increase in lattice parameters and cell volume as a function of the BNN fraction [31–33].
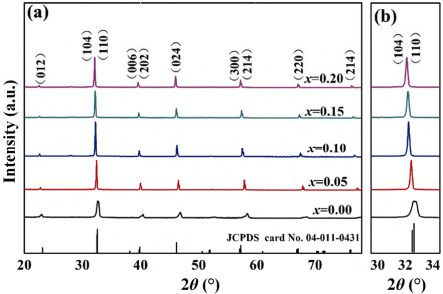
Fig. 1 (a) XRD patterns of pure and BaNi0.5Nb0.5O3-modified Bi0.5Na0.5TiO3 ceramics; (b) locally magnified patterns at 2θ = 30°–34°.
The SEM analyses were performed for the (1–x)Bi0.5Na0.5TiO3–xBaNi0.5Nb0.5O3 (BNT–BNN; 0.00 ≤ x ≤ 0.20) ceramic morphology in Fig. 2. Figure 2 illustrates a typical 3000× SEM micrograph of sample ceramics with highly dense and free-void grains. It can be seen from the figure that x = 0.05 has a denser morphology and the smallest grain size. Generally, the photovoltaic effect in ferroelectric materials correlates with the grain size effect [5]. The full density and homogenous microstructures with small grain size are the important factor on the improvement of photocurrent. It is believed that the smaller grain size of the samples will form more defects in grain boundary, which can provide more absorbing centers inside the samples. The carriers will be trapped inside the samples, which will form an electro-potential barrier and lead to the larger photocurrent [34].

Fig. 2 SEM images of the (1–x)Bi0.5Na0.5TiO3–xBaNi0.5Nb0.5O3 (BNT–BNN; 0.00 ≤ x ≤ 0.20).
The Raman diffraction is an advantageous mean of characterization, which can provide accurate information about the local deformation and ion configuration in the crystal structure. At ambient temperature, Fig. 3(a) represents the Raman scattering spectra of (1–x)BNT–xBNN (x = 0.00–0.20) ceramic samples in a wave number from 100 to 1000 cm-1. About four regions were detected in the spectra, and they are nearly identical to those previously reported for BNT-based ceramics [35]. Figure 3(b) exhibits the Raman spectroscopy of the x = 0.05 ceramic sample fitted by Gaussian peak functions. The measured region (100–1000 cm-1) of the ceramic samples can be deconvoluted into six main peaks, which are located at 116, 273, 524, 600, 727, and 790 cm-1. The peak at 116 cm-1 is mainly affected by the Na–O bonds of the A-site vibration in the ABO3 style perovskite ceramics [36]. The peak at 274 cm-1 is only related to the bending motion of O–Ti–O, which is also very susceptible to phase transformation [37,38]. The Raman peak in the range of 400–700 cm-1 is mainly attributed to the stretching symmetric vibration mode of TiO6 octahedron [39]. After 700 cm-1, the Raman peak is mainly related to the two longitudinal optical overlapped peaks, A1 (longitudinal optical) and E (longitudinal optical) [40]. The XRD patterns and Raman analysis indicate that the BaNi0.5Nb0.5O3 can be incorporated into the Bi0.5Na0.5TiO3 matrix to form a new solid solution.
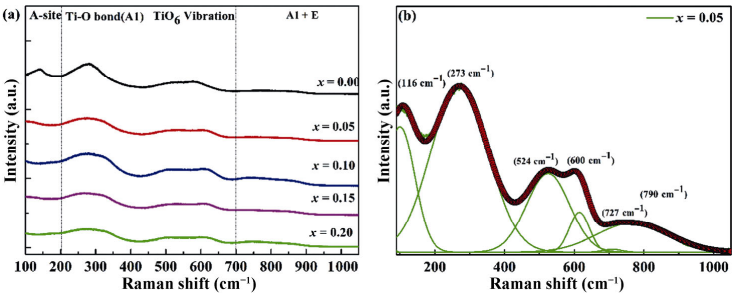
Fig. 3 (a) Raman scattering spectra of the ceramic samples; (b) Raman deconvolution of x = 0.05 sample.
Figure 4 illustrates the polarization loops of (1–x)BNT–xBNN ceramic samples with x = 0.00–0.20. All the ceramics show typical ferroelectric hysteresis loops. With the increasing x, the maximum residual polarization value (Pr) and the coercive field (Ec) of the ceramics decrease gradually. The decrease of Pr can mainly be due to the phase transition from ferroelectric to paraelectric [41]. Oxygen vacancy led to this phenomenon. The substitution of Ti5+ by Ni2+ results in the long-range ordered displacement of Ti5+ and structural local strain. Considering the electronegativity of Ba and Na, the ionic strength of the modified A–O bond is partially replaced with Ba2+ at the A-site. Furthermore, with the change of the grain size of the ceramic samples, the grain boundary and defects will have pinning effect on the domain and lead to the decrease of Ec [42].
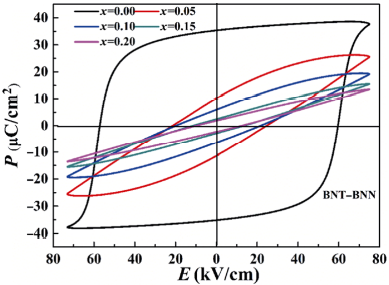
Fig. 4 Electric induced polarization loops (P–E) of (1–x)BNT–xBNN (x = 0–0.20) ceramic samples.
Figures 5(a)–5(e) illustrate the change of the dielectric constant (εr) and dielectric loss (tanδ) of the ceramic samples in different frequency ranges with temperature. It can be observed that with the increase of temperature, εr increases gradually, reaches the maximum value at Curie temperature (TC), and then decreases gradually. At the same time, before the TC, the relative permittivity of low-frequency gradually increases with the increase of the test temperature, which may be related to the polarization and conductivity of space charges in the samples [43]. The tanδ increases sharply above ~TC. It could be due to the loss of some bismuth and sodium oxide during the sintering process, as well as the resulting defect chemical changes, resulting in ionic and electronic conduction inside the samples, which causes the rise in tanδ [44,45].
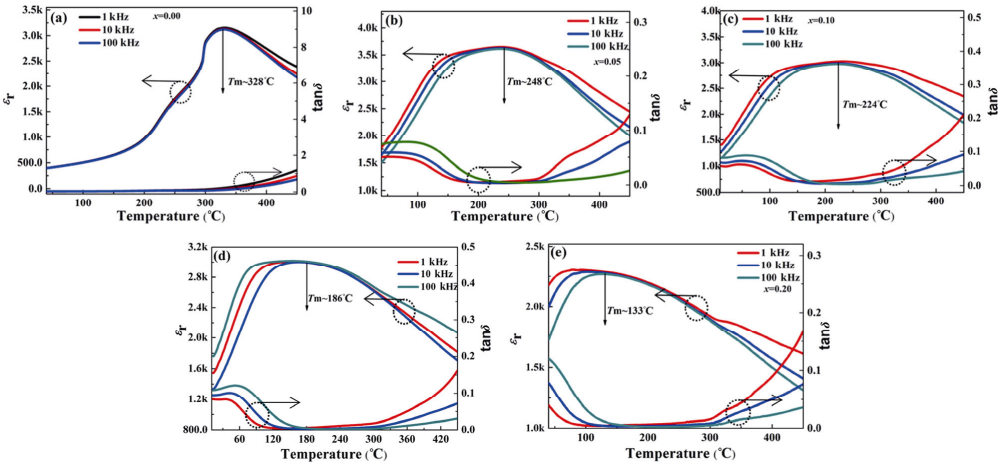
Fig. 5 Relative permittivity and tanδ versus temperatures for the ceramic samples: (a) pure BNT, (b) 0.95BNT–0.05BNN, (c) 0.90BNT–0.10BNN, (d) 0.85BNT–0.15BNN, (e) 0.80BNT–0.20BNN.
Complex impedance spectroscopy (CIS) is an effective method to detect the electrical properties of conductive interface for ceramics. At the same time, it can also be used to analyze moving charge carriers and bond dynamics in solid or liquid mixtures (insulating layer, semiconductor, ion). Moreover, the physical process inside the sample can be identified by the corresponding equivalent circuit model [46]. Figures 6(a) and 6(b) illustrate the Cole–Cole plots of 0.95BNT–0.05BNN ceramics from 400 to 650 ℃. The Cole–Cole plots can be fitted by two parallel R–CPE–C elements connected in series in inset of Fig. 6(a). It can be observed that the radius of the arcs gradually decreases with increasing temperature, indicating the resistance of 0.95BNT–0.05BNN ceramic decreases with the increase of the test temperature. The result can also reflect these ceramic samples have the negative temperature coefficient of resistance (NTCR) effect. In order to evaluate the rationality of the equivalent circuit and the accuracy of fitting data, we calculated the impedance residuals of Z′ and Z″, which reflect the difference between experimental and fitting data, as show in Fig. 6(c). Residual values of Z′ and Z″ are in the range of (−0.0001)–(+0.0003), suggesting that the fitting data are reliable. Figure 6(d) illustrates the Arrhenius-type plots of 0.95BNT–0.05BNN ceramic. Through the formula: σ = H/(RS), the conductivity of grain and grain boundary can be calculated, where H represents the thickness of the ceramic, R represents the grain resistance or grain boundary resistance, and S represents the surface area of electrode. And then, the activation energies of ~0.61 and 0.68 eV of the grains (Eag) and the grain boundaries (Eagb) are worked out by the Arrhenius-type curves, respectively. The magnitude of activation energy denotes that the conductive species of grains and grain boundaries in the ceramic samples are ascribed to the double ionized oxygen vacancies [47,48]. The formation of doubly ionized oxygen vacancies can be expressed by Kröger-Vink notation, as given below:

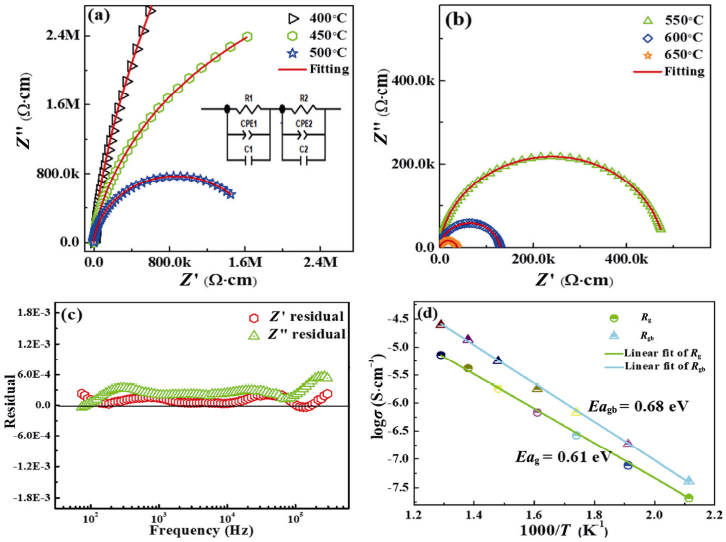
Fig. 6 Cole–Cole plots of 0.95BNT–0.05BNN ceramic samples were measured at temperatures of (a) 400–500 ℃ and (b) 550–650 ℃. The inset in (a) illustrates the fitting circuit model; (c) illustrates the impedance residuals of Z′ and Z″; (d) illustrates the Arrhenius-type plots of 0.95BNT–0.05BNN ceramic under air atmosphere.
The optical properties of the ceramic samples are observed via the UV–Vis–NIR spectra. The light absorption of the all samples is shown in Fig. 7(a). Compared to pure Bi0.5Na0.5TiO3 ceramic, the BaNi0.5Nb0.5O3-doped Bi0.5Na0.5TiO3 ceramics show broad light absorption spectrometer covering the range from visible light down to near-infrared (NIR) (λ < 1600 nm). Meanwhile, the light absorption efficiency of the ceramics improves as the doping content increases. This material exhibits more potential advantages in the photovoltaic field. In Fig. 7(b), the optical bandgaps (Eg) of BaNi0.5Nb0.5O3-doped Bi0.5Na0.5TiO3 ceramics are determined by (αhν)² = A(hν–Eg), showing that the samples have three gap states corresponding to the absorption spectrum in Fig. 7(a) [40]. In the UV–Vis part, the band gaps decrease from 3.1 to 2.27 eV, which is lower than that of the typical BNT–SF ceramics (2.4 eV for 9 mol% Sr/Fe-added) [49]. The reduction in the optical bandgap may be related to the introduction of Ni ions. There is an obvious midgap state corresponding to Ni 3d between valence band maximum (VBM) of Ti 3d and conductive band minimum (CBM) of O 2p. Doping transition metals in Bi0.5Na0.5TiO3 materials is predicted to generate a localized state between the bottom of conductive band and the top of valence band to reduce the optical bandgap, and the bandgap tuning mechanism with introduction of Ni ions is shown in the inset of Fig. 7(b) [50]. Therefore, the light absorption range of the samples can significantly broaden and the band gap can be reduced by the proper doping.
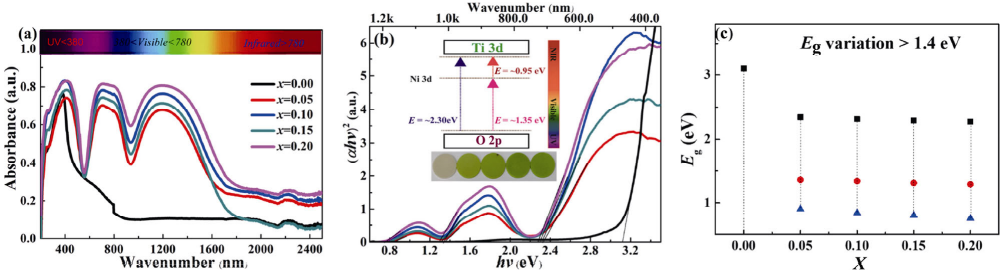
Fig. 7 (a) Absorbance spectra of pure and BNN-modified BNT materials. The inserted color bar was used to show the
absorption at UV, visible, and NIR range; (b) band gap of (1–x)BNT–xBNN (x = 0.00–0.20) ceramic samples. The inset in (b)
illustrates the bandgap tuning mechanism of the samples; (c) three sub-bandgap values of (1–x)BNT–xBNN (x = 0.00–0.20)
ceramic samples are shown and dotted line shows the variation between the gap states of the samples.
In this system, the 0.95BNT–0.05BNN ceramic has relatively high residual polarization strength, low band gap, and the largest Jsc. So, this component was selected for systematic study. The photocurrent density–voltage (J–V) curves measured both in the dark and under light illumination for 0.95BNT–0.05BNN ceramic are presented in Fig. 8(a). In the dark, the sample show near-zero dark current, while its photocurrent is clearly enhanced under light irradiation, a small open-circuit voltage (Voc) of ~15.7 V and a short-circuit current density (Jsc) of ~1450 nA/cm² are obtained. Under the same measurement conditions, the Jsc and Voc of x = 0.00, 0.10, 0.15, 0.20 compositions are 20.00, 1220, 1060, 930 nA/cm² and 2.0, 13.1, 11.5, 8.4 V, respectively. The photocurrent density for various compositions is presented in Table 1. The improvement of photocurrent in illumination can be attributed to the photo-generated carriers. The structural mechanism diagram of the ITO/BNNT/Ag device is shown in Fig. 8(e, upper). The 0.95BNT–0.05BNN ceramic is poled under the different poling field for 10 min in Fig. 8(b). The photocurrent gradually increases with the increase of poling field from 30 to 60 kV/cm. The sample was exposed to a polarized electric field of 60 kV/cm for 10 min; the greatly improved Jsc of ~5500 nA/cm² is obtained, which is 4 times higher than that of unpoled sample. To further analyze the effect of light intensity on photocurrent density, the light intensity-dependence of the output current is shown in Fig. 8(c). It can be observed from Fig. 8(c) that the output photocurrent gradually increases with the increase of light intensity from 50 to 200 mW/cm². This indicates that the light intensity can affect the activity of photogenerated carriers and further promote their separation, thus increasing the output current. It is reported that photocurrent density depends on many factors including bandgap, carrier mobility, wavelength, and intensity of light [51]. For ferroelectric semiconductors, the photocurrent is due to the following factors, including the large residual polarization combined with a narrow band gap (Eg) and the Schottky barrier at the electrode interface of the ceramic samples [52]. It is easy to form Schottky barrier built-in field (Ebi) on unpolarized ITO/0.95BNT–0.05BNN/Ag devices. The net built-in electric field (Ebi) in the ITO/0.95BNT–0.05BNN/Ag device is from Ag to ITO because the Schottky barrier of ITO/0.95BNT–0.05BNN interface is much higher than that of Ag/0.95BNT–0.05BNN interface, as shown in Figs. 8(a)–8(e). The Ebi provides the driving force for photogenerated electron–hole pair separation in the bulk ceramic and induces the interface photovoltaic effects in unpoled 0.95BNT–0.05BNN ceramic. After positive poling, the depolarization electric field (Edp) existing in the entire ferroelectrics has the same direction as the Ebi, which is beneficial for the separation of photogenerated electron–hole pairs, as shown in Figs. 8(b)–8(e). Therefore, a higher Jsc is obtained in the poled 0.95BNT–0.05BNN ceramic. The photocurrent and dark-current density conversion of 0.95BNT–0.05BNN ceramic is illustrated in Fig. 8(d). The observed photocurrent exhibits a fast and repeatable photo-response effect, just in line with the on/off photo-period. The results show that the BNT–BNN system is a promising candidate in the field of photovoltaics and photosensitive devices [53].
Table 1 Photocurrent density of (1–x)BNT–xBNN (x = 0.00–0.20) ceramics
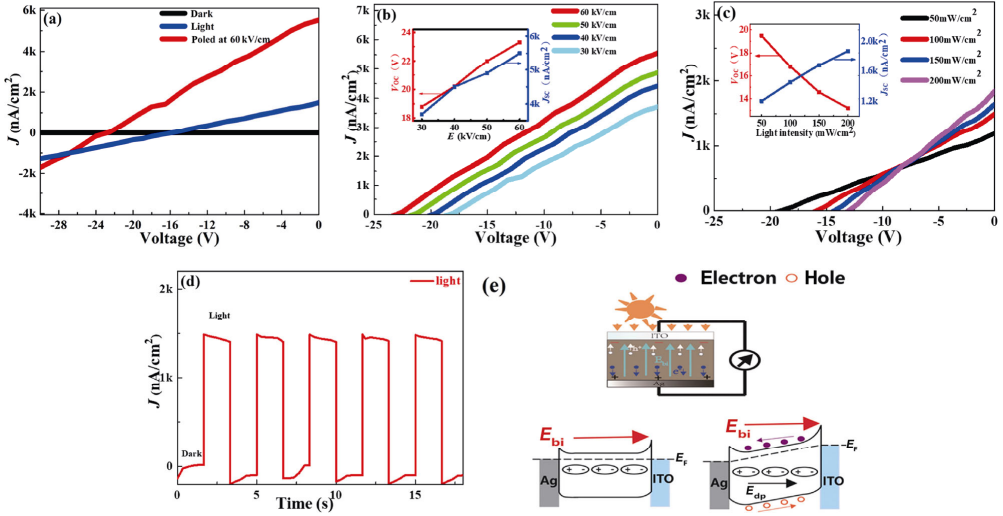
Fig. 8 (a) J–V curves under simulated AM1.5 sunlight of 100 mW/cm² for the 0.95BNT–0.05BNN sample; (b) J–V curves under different poling field for the 0.95BNT–0.05BNN ceramic at room temperature. The inset illustrates the open circuit voltage Voc and short circuit current Jsc under different poling field; (c) J–V curves under different optical power densities of 0.95BNT–0.05BNN sample. The inset illustrates the open circuit voltage Voc and short circuit current Jsc with different optical power densities; (d) photocurrent switching plots with the time of 0.95BNT–0.05BNN ceramic at room temperature; (e) structural mechanism diagram of the ITO/BNNT/Ag device is shown in the upper, and the electronic band diagram of the sample
device in the polarization state is shown in the bottom.
4 Conclusions
The (1–x)BNT–xBNN materials with x = 0.00–0.20 were successfully fabricated using the solid-state technique. This article systematically studies the crystal structures, photovoltaic properties, and electrical characteristics of the system. The main phase of structure in the samples shows a perovskite crystalline structure. The ferroelectric properties of all samples at room temperature are verified by ferroelectric hysteresis. TC ranges from 330 to 120 ℃ with increasing x. The BNT–BNN ceramics show low tanδ (≤ 0.1) in the wide temperature range of 100–300 ℃. Observing from Cole–Cole plots, the sample had NTCR properties. The absorbance in the visible region has been significantly improved, and the band gap has been reduced from 3.1 to 2.27 eV. Under simulated sunlight illumination (AM1.5G, 100 mW/cm²), a large Jsc of 1450 nA/cm² and a small Voc of ~15.7 V can be obtained. A larger Voc of 23 V and a higher Jsc of 5500 nA/cm² are achieved at the poling field of 60 kV/cm under the same light conditions. Superior optical properties make BNT–BNN ceramics an ideal candidate for photovoltaic applications. Our results have application potential in the field of ferroelectric photovoltaic.
References: omitted
Declaration: This article is provided by CERADIR™ users or obtained from Internet, the content does not represent the position of CERADIR™. We are not responsible for the authenticity/accuracy of the article, especially the effects of the products concerned. This article is for study only, it does not constitute any investment or application advice. For reprinting, please contact the original author. If it involves the copyright and/or other issues, please contact us and we will deal with it asap! CERADIR™ has the interpretation of this declaration.







