摘要:陶瓷的压缩破坏是一个爆炸式破碎的过程,在短时间内急剧释放大量能量,并伴随大量高速飞行碎片的产生,实验上较难获取陶瓷压缩破坏过程中碎片的飞溅速度。本文采用离散元数值模拟氧化铝陶瓷的压缩破碎过程,分析了不同应变率下产生碎片的尺寸分布、碎片的平均飞溅速度,以及试件内部不同区域碎片的速度变化规律。研究表明:(1)陶瓷的表观破坏强度以及破碎后碎片的平均飞溅速度与加载应变率正相关;(2)碎片飞溅速度与其初始位置相关,外侧碎片的飞散速度最大,随着初始位置与试件中心轴距离的减小,碎片飞溅速度逐渐减小;(3)随着加载应变率的提高,碎裂产生的碎片数逐渐增多,对应的碎片平均尺寸变小。进一步讨论了试件压缩破碎过程中的能量守恒和转换模式,并对碎片飞溅的平均速度进行了理论分析。
关键词: 陶瓷, 压缩破坏, 离散元, 碎片飞溅速度, 碎片尺寸, 能量转换
0 引 言
陶瓷材料由于自身优异的性能,在防护工程、航空航天和国防民用领域都有广泛应用,国内外研究人员对陶瓷材料的动态力学性能及其破坏强度进行了较系统地研究[1-4]。陶瓷材料的破坏强度通常表现出明显的应变率效应,即随着应变率的增加,陶瓷材料的破坏强度也随之提升[5]。在冲击荷载作用下,由于加载时间和应力波的传播及裂纹的发展时间相近,材料通常会破碎成多个碎片,并且碎片的特征尺寸与应变率相关[6]。陶瓷材料的压缩强度显著大于拉伸强度[7],通常具有量级上的差别,在工程应用上,陶瓷材料常作为承压部件来使用。 而陶瓷材料强烈的拉压不对称特性,导致其在压缩荷载作用下一旦发生破坏,试件内部积累的大量弹性势能将在非常短的时间内全部释放,破碎形式为一瞬间的爆炸式破坏,并且通常都伴随着大量碎片高速飞溅[8-9]。长期以来,对脆性材料在冲击载荷作用下的碎裂特征,尤其是碎片尺寸和碎片飞行速度受到广大科研工作者们的重点关注。 在给定外载条件下,对脆性碎裂过程产生的碎片尺寸分析可以为岩爆、采矿等工程设计提供一定参考,而对碎片飞溅速度分析能进一步了解碎片所携带的能量和破坏过程中的能量转换,亦可为陶瓷装甲结构的抗冲击性能研究提供一定思路。 冲击碎裂过程中产生的碎片尺寸可以通过试验后的碎片回收测量统计获得,但陶瓷类脆性材料冲击碎裂的细致过程难以通过试验观察获得,而在使用高速摄影机拍摄过程中,由于时空分辨率不足等因素的限制,也难以清晰地了解其内部的破坏过程,因而无法准确判断碎片的飞行速度。
在数值模拟方面, 普遍采用传统的有限元数值方法对陶瓷材料进行数值分析。吴雪等[10] 采用AUTODYN 研究了具有预应力的陶瓷的抗侵彻性能,得到了不同加载下陶瓷内部的应力分布和其抗侵彻能力与预应力的关系。冯晓伟等[11]数值模拟了平板冲击压缩下陶瓷材料的细观破坏过程,分析了破坏波在陶瓷内部的传播机理。杨震琦等[12]采用 LS-DYNA 数值模拟了氧化铝陶瓷在低速冲击载荷下的损伤演化和破坏行为,得到陶瓷在冲击压缩下的破坏模式主要为轴向劈裂的结果。Zhou 等[13] 采用内聚力断裂模型数值分析了脆性材料在冲击拉伸载荷作用下的碎裂行为,获得了碎片尺寸与加载应变率的经验公式。 但是在冲击压缩载荷作用下,当材料压缩破坏时,由于有限元单元分离之后仍然处于压剪状态,大量碎片之间将形成数量庞大的接触面,在计算过程中常常会造成网格穿透,使计算结果不稳定和不准确,故采用内聚力断裂模型计算脆性材料的压缩碎裂问题还有待进一步提高[14]。
另一方面,由于非连续粒子集合的动力学算法在处理碎裂的复杂问题上具有独特的优势,许多学者也采用离散元、分子动力学等颗粒动力学方法来模拟陶瓷材料的压缩破碎过程。成琴等[15] 采用分子动力学方法,从微观角度对不同晶粒尺寸的 β-SiC 陶瓷的破坏模式进行研究;姜胜强等[16]采用颗粒流软件 PFC2D对陶瓷加工过程中的划痕试验进行数值模拟,得到了预应力对陶瓷切削过程中裂纹扩展的影响规律;Gusev[17]、Yu 等[18]采用格点-弹簧模型对脆性材料的冲击压缩过程进行了数值模拟;吕文银等[19]对陶瓷材料的细观破坏过程进行了模拟,探索了孔隙对陶瓷材料压缩力学性能的影响,但建立的格点弹簧模型计算量庞大。
上述工作均未进一步分析材料压缩破坏后的碎片大位移飞溅过程和碎片飞溅速度的分布规律。因此,本文采用离散单元法,对氧化铝陶瓷材料压缩碎裂过程进行三维数值模拟,数值再现压缩破碎后的碎片大位移运动过程,重点关注碎裂中碎片尺寸分布和飞溅速度分布规律、影响因素及内在机理。
1 离散元模型
本文选取的 Al2O3 陶瓷的几何模型为 ϕ10 × 10 mm的圆柱体,通过离散单元法建立散体颗粒模型,考虑颗粒几何匹配良好,粒径分布范围为 0. 2 ~ 0. 8 mm,离散颗粒总数为 56 304 个,具体模型如图 1 所示。陶瓷试件下端面设为固定端,试件侧向为自由表面,在试件上端面施加速度向下的表面压力对陶瓷进行压缩。模拟分析陶瓷的压缩破坏过程,通过对颗粒单元的微观运动进行追踪计算,讨论压缩破碎过程中产生碎片的宏观运动规律及力学响应。

图 1 圆柱陶瓷试件的离散元模型
颗粒之间的接触选用离散元模型中常用的Hertz-Mindlin 粘结模型。根据文献[20]中 Al2O3 的准静态压缩力学行为对离散元微观参数进行标定,其结果如表 1 所示。
表 1 Hertz-Mindlin 粘结模型的关键参数

2 结果与讨论
2. 1 压缩过程中的应变率效应
由于离散元计算通常耗时较长,为节省计算时间,数值计算中采取了较高的压缩速度,即对试件的上端面施加 50 m/ s、100 m/ s、200 m/ s、500 m/ s 的压缩速度,分别对应的初始压缩应变率为 5 × 10³ s-1、1 × 104 s-1、2 ×104 s-1、5 ×104 s-1。图 2 为不同应变率加载下陶瓷的应力时程曲线,从图中可以看到,随着应变率的升高,陶瓷的压缩破坏强度显著提高,表明 Al2O3 陶瓷具有明显的应变率效应。 并且加载速率越大,应力振荡幅值越大,表明陶瓷试件内部破坏剧烈并且局部应力不平衡。
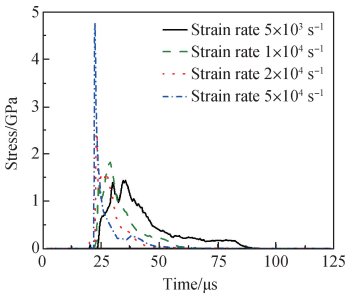
图 2 不同应变率加载下陶瓷的应力时程曲线
陶瓷试件压缩破坏瞬间,由一个整体瞬间碎裂为无数个碎片,图 3 给出了 Al2O3 陶瓷在不同应变率加载下产生碎片的飞溅形态。碎片的尺寸和速度代表了其内部能量转换,与材料断裂韧性、断裂应变能大小、外界做功等直接相关。 随着应变率的增大,陶瓷压缩破坏后的碎裂程度更加剧烈,碎片平均尺度更小,这与试验现象结果一致[20]。同时,可以发现随着应变率的提高,碎片的平均飞溅速度增大,尤其是外侧碎片的飞溅速度显著提高。
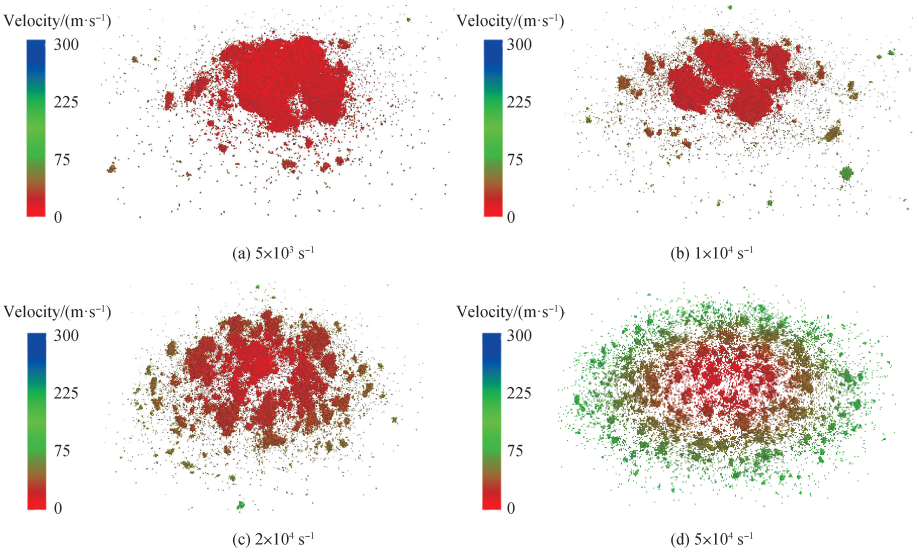
图 3 不同应变率加载下陶瓷碎片速度云图
图 4 为不同应变率加载下陶瓷压缩强度和碎片平均飞溅速度,Al2O3 陶瓷在不同的应变率压缩破坏过程中表现出显著的应变率敏感特性,其表观压缩强度随应变率的提高而几乎呈线性增加,在应变率为 5 × 104 s-1时压缩强度接近 5 GPa,比试验获得的压缩强度高,压缩试验过程中试件端面常常会应力集中,从而导致陶瓷类高强高硬材料的动态强度被低估[21]。碎片平均飞溅速度也随应变率的提高而显著增大,更高应变率加载带来的额外能量被转化为了动能,使得碎片的飞溅速度更大。
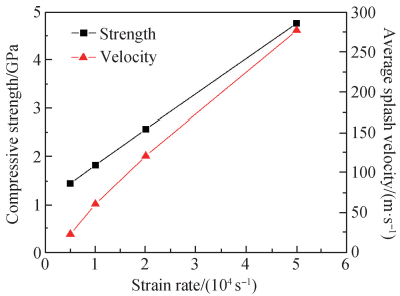
图 4 不同应变率加载下陶瓷压缩强度和碎片平均飞溅速度
2. 2 碎裂过程产生的碎片尺寸分布
对不同加载应变率下的 Al2O3 陶瓷碎裂过程产生的碎片进行统计,如表 2 所示。 整体而言,Al2O3 陶瓷在压缩过程中内部存储了大量的应变能,而陶瓷的断裂能又极低,碎裂过程中产生了大量的碎片,并且多为小尺寸碎片。 随着加载应变率的提高,碎裂产生的碎片数逐渐增多,对应的碎片平均尺寸变小。
表 2 不同应变率加载下产生的碎片尺寸统计
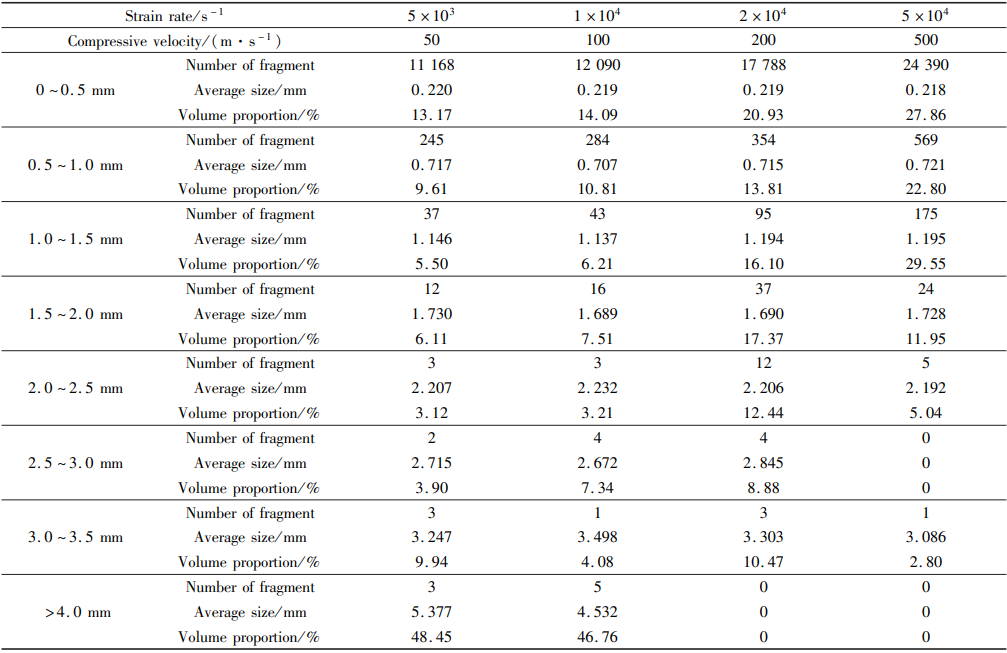
图 5 给出了不同加载应变率下碎片粒径的体积占比,从图中可以看出:当应变率在 1 × 104 s-1以下时,碎裂过程产生了若干直径超过 4 mm 的大体积碎片,并且体积占比接近 50% ;而当应变率在 2 × 104 s-1以上时,碎裂过程没有产生大体积碎片,并且随着应变率的提高碎片分布均值朝小尺寸移动。 Al2O3 陶瓷在压缩过程中发生爆炸式的破坏,大量高速飞溅的微小碎片带走了较多的能量,在试件中心位置的陶瓷材料不再发生严重的碎裂现象,会残留部分较大尺寸的陶瓷碎片;而更高应变率加载使得冲击破碎过程更加的剧烈,外侧碎片的破坏不足以卸载更多的外载能量,陶瓷内部进一步发生粉碎式的碎裂,碎片尺寸均值更趋于小值。
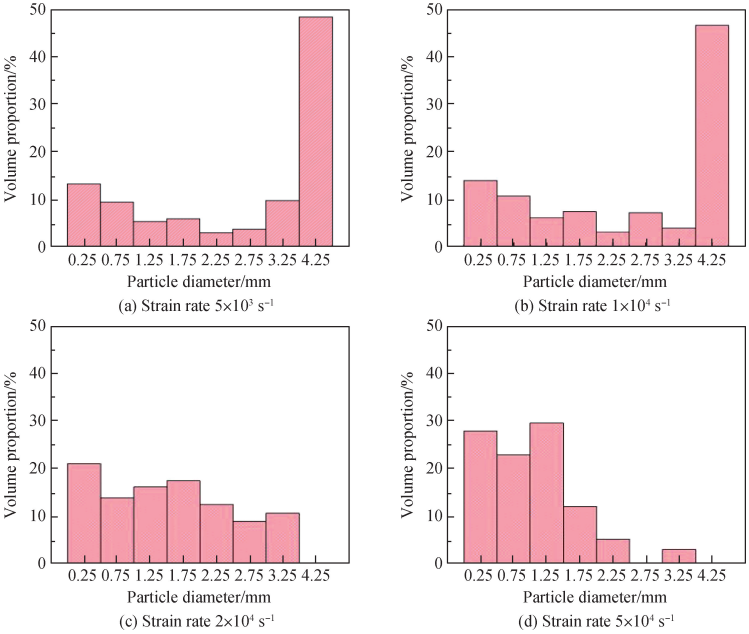
图 5 碎片粒径与体积比的关系
2. 3 压缩过程中碎片飞溅速度规律
选取应变率为 2 × 104 s-1的工况为典型代表,当陶瓷发生压缩破碎后,随机选取压缩过程中产生的若干碎片,对其运动规律进行分析。 通过反向追踪获得各个碎片在陶瓷试件中的原始位置,其原始位置在水平面的投影坐标如图 6 所示。
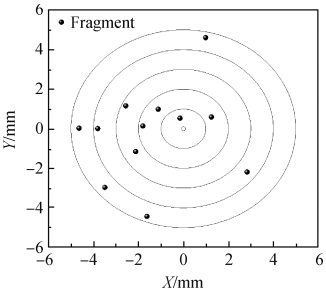
图 6 碎片原始位置示意图
图 7 给出了与陶瓷中心轴距离不同的部分碎片的速度时程曲线,显然,距离试件中心轴较远的碎片,其飞溅速度峰值和最后的稳定飞行速度均比距离试件中心轴较近的碎片要大,离试件中心轴 4. 7 mm 的外侧碎片飞溅速度接近 250 m / s,而离试件中心轴 1. 8 mm 的内部碎片速度只有大约 20 m / s。同时,将碎片速度增长初期阶段曲线放大,可以发现碎片速度增长率也和碎片的初始位置相关,试件外侧粒子的速度增长率显著高于内部粒子的速度增长率。将陶瓷压缩碎裂过程等效为“压缩劈裂-径向膨胀-拉伸碎裂”过程[9],试件的弹性压缩应变产生的泊松膨胀效应导致了碎片的径向飞溅,外侧碎片由于处于初始自由面位置,将获得更高的飞行速度,内部碎片相对获得的速度更低。并且,试件发生破碎之后,各碎片的速度发生剧烈变化,碎片间也存在不可避免的相互碰撞,因此速度呈现一定的振荡直至最后稳定。
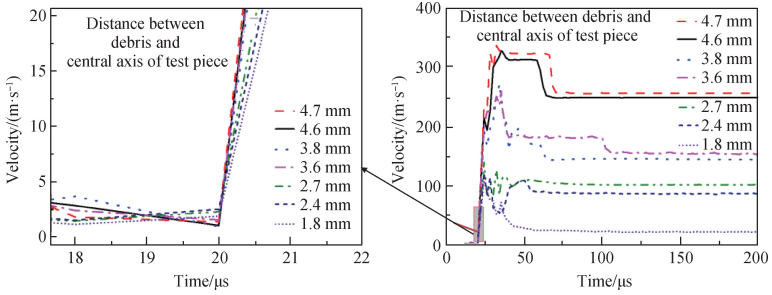
图 7 不同位置碎片的速度时程曲线
图 8 为碎片稳定飞行的速度与其初始位置之间的关系。从图中可以看出,陶瓷破碎后产生的所有碎片的稳定飞行速度平均值大约在 120 m / s,单个碎片稳定飞行速度和其与试件中心轴的初始距离之间近似为线性关系。陶瓷圆柱试件在单轴压缩载荷作用下发生的破碎过程,可以近似认为是径向方向的恒应变率膨胀过程。通过对图 8 中各碎片的速度进行线性拟合,从而得到试件的横向膨胀速率,即线性拟合的斜率,其值约为 6. 5 × 104 s-1,显然比施加在试件上端面的轴向加载应变率 2 × 104 s-1要高得多。造成该现象的主要原因是在压缩初期试件内部存储了大量的应变能,而陶瓷的断裂韧性又极低,裂纹一旦产生,试件整体将会在极短的时间内完成一次爆炸式的破碎过程。
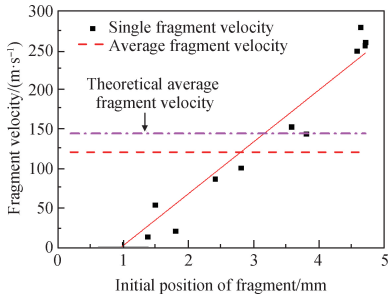
图 8 碎片稳定飞行的速度与其初始位置之间的关系
2. 4 压缩变形-破碎过程的能量转换
根据能量守恒可知,在压缩破坏之前,外界做功应该完全转化为陶瓷试件内部的应变能和变形运动的附带动能,而陶瓷一旦瞬间破坏,上述总能量将转化为碎片的飞溅动能和断裂表面能。 即
W = Uε + K = G + Ep (1)
式中:W 为外界做功;Uε 为陶瓷压缩过程中积累的弹性应变能;K 为陶瓷试件破坏前的动能;G 为陶瓷碎裂消耗的断裂能;Ep 为所有碎片的动能总和。
通常陶瓷类脆性材料的破坏均是弹脆性破坏,即式中:V 为陶瓷试件的体积;E 为弹性模量;σc 为陶瓷的压缩极限强度。

而在动态压缩过程中,由于试件上端面具有向下的压缩速度,而试件下端面为固定端,即速度为 0,因此,在压缩过程中试件压缩变形带来的附加动能为
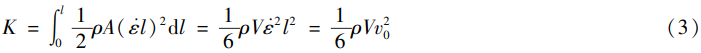
式中:ρ 为陶瓷密度;A 为圆柱试件的横截面积;ε̇ 为压缩应变率;l 为圆柱试件长度;v0 为试件上端面压缩速度。根据文献[9]可知,陶瓷在压缩过程中的断裂能占总能量的比值不到 5% ,因此本文忽略陶瓷破坏消耗的断裂能,近似可得

因此碎片的平均飞溅速度(v)为

以应变率为 2 × 104 s-1 的试件破碎后的碎片为例,其中陶瓷密度 ρ = 2 722 kg/m³,陶瓷弹性模量E = 321 GPa,该应变率下陶瓷的压缩强度 σc = 2. 57 GPa,试件上端面压缩速度 v0 = 200 m / s,从而得到陶瓷试件破碎后的碎片平均速度约为 145 m / s,略高于数值模拟中获得的碎片平均速度(见图 8)。两者之间的差异主要来自以下两方面:(1)在能量平衡关系中,忽略了断裂能的耗散和破碎过程激发的内部应力波能量,从而将该部分能量计算到碎片动能部分;(2)对于具有一定速度分布的碎片群体,采用单个碎片飞溅速度的平均值通常会使碎片群体携带的动能总量被低估。
3 结 论
(1)陶瓷试件的表观破坏强度以及破碎后的碎片平均飞溅速度与加载应变率正相关,表明陶瓷材料具有明显的应变率效应。
(2)Al2O3 陶瓷在压缩过程中发生爆炸式的破坏,破坏后产生了大量尺寸集中在 0 ~ 1. 0 mm 的小碎片,并且总体的碎片尺寸分布与加载应变率显著相关,随着应变率的提高碎片分布的均值朝小尺寸移动。
(3)陶瓷试件在压缩破碎过程中,碎片飞溅速度体现出显著的空间分布特性,依赖于碎片的初始位置高度,外侧碎片的飞散速度最大,随着初始位置与试件中心轴距离的减小,碎片飞溅速度逐渐降低。径向方向的膨胀速率高于轴向方向的压缩速率,表明试件瞬间的爆炸式破坏的主要原因是内部积累的大量弹性势能在极短的时间内快速释放。
参考文献:
[1] WANG H, RAMESH K T. Dynamic strength and fragmentation of hot-pressed silicon carbide under uniaxial compression[J]. Acta Materialia, 2004, 52(2): 355-367.
[2] SARVA S, NEMAT-NASSER S. Dynamic compressive strength of silicon carbide under uniaxial compression[J]. Materials Science and Engineering: A, 2001, 317(1/2): 140-144.
[3] 李英雷,胡时胜,李英华.A95陶瓷材料的动态压缩测试研究[J].爆炸与冲击,2004,24(3):233-239.
[4] 王永刚,周风华.径向膨胀Al2O3陶瓷环动态拉伸破碎的实验研究[J].固体力学学报,2008,29(3):245-249.
[5] ZHOU F H, MOLINARI J F. Stochastic fracture of ceramics under dynamic tensile loading[J]. International Journal of Solids and Structures, 2004, 41(22/23): 6573-6596.
[6] GLENN L A, CHUDNOVSKY A. Strain-energy effects on dynamic fragmentation[J]. Journal of Applied Physics, 1986, 59(4): 1379-1380.
[7] ROSENBERG Z. On the relation between the Hugoniot elastic limit and the yield strength of brittle materials[J]. Journal of Applied Physics, 1993, 74(1): 752-753.
[8] 张青艳,靳晓庆,周风华.Al2O3陶瓷柱在准静态压缩下的破坏和动态碎裂过程[J].兵工学报,2013,34 (1):151-156.
[9] ZHANG Q Y, ZHENG Y X, ZHOU F H, et al. Fragmentations of alumina (Al2O3) and silicon carbide (SiC) under quasi-static compression[J]. International Journal of Mechanical Sciences, 2020, 167: 105119.
[10] 吴 雪,张先锋,丁 力,等.预应力对陶瓷抗侵彻性能影响规律的数值模拟[J].高压物理学报,2018,32(4):75-82.
[11] 冯晓伟,李俊承,常敬臻,等.氧化铝陶瓷受冲击压缩破坏的细观机理研究[J].兵工学报,2017,38(12):2472-2479.
[12] 杨震琦,庞宝君,王立闻,等.JH-2模型及其在Al2O3陶瓷低速撞击数值模拟中的应用[J].爆炸与冲击,2010,30(5):463-471.
[13] ZHOU F, MOLINARI J F. Dynamic crack propagation with cohesive elements: a methodology to address mesh dependency[J]. International Journal for Numerical Methods in Engineering, 2004, 59(1): 1-24.
[14] ZHOU F H, MOLINARI J. F. Numerical investigation of dynamic compressive loading[J]. Ceramic Engineering and Science Proceedings, 2003, 24(3): 417-423.
[15] 成 琴,吴恒安,王 宇,等.β-SiC陶瓷材料增韧机制的分子动力学模拟[J].中国科学技术大学学报,2010,40(12):1267-1272.
[16] 姜胜强,谭援强,聂时君,等.碳化硅陶瓷预应力加工的离散元模拟与实验研究[J].无机材料学报,2010,25(12):1286-1290.
[17] GUSEV A A. Finite element mapping for spring network representations of the mechanics of solids[J]. Physical Review Letters, 2004, 93(3): 034302.
[18] YU Y, WANG W Q, HE H L, et al. Modeling multiscale evolution of numerous voids in shocked brittle material[J]. Physical Review E, Statistical, Nonlinear, and Soft Matter Physics, 2014, 89(4): 043309.
[19] 吕文银,张青艳,周风华.基于格点-弹簧模型模拟含缺陷陶瓷材料的压缩破坏过程[J].宁波大学学报(理工版),2017,30(5):76-82.
[20] 张青艳.脆性材料在准静态和冲击压缩载荷作用下的动态碎裂过程[D].宁波:宁波大学,2019.
[21] 陈为农,宋 博.分离式霍普金森(考尔斯基)杆[M].姜锡权,卢玉斌译.北京:国防工业出版社,2018.
声明:本文由 CERADIR 先进陶瓷在线平台的入驻企业/个人提供或自网络获取,文章内容仅代表作者本人,不代表本网站及 CERADIR 立场,本站不对文章内容真实性、准确性等负责,尤其不对文中产品有关功能性、效果等提供担保。本站提醒读者,文章仅供学习参考,不构成任何投资及应用建议。如需转载,请联系原作者。如涉及作品内容、版权和其它问题,请与我们联系,我们将在第一时间处理!本站拥有对此声明的最终解释权。













