摘要:聚合物空间稳定机制是陶瓷悬浮液稳定的主要方式。本文以聚合物空间稳定的氧化铝悬浮液为研究对象,通过流变性能测试,研究了悬浮液体积分数、聚合物含量、颗粒粒径对悬浮液弹性模量的影响规律。结果表明,稳态剪切和振荡剪切两种流变测试模式都证明了悬浮液存在明显的弹性特征。确定了对于聚合物稳定的氧化铝悬浮液,影响弹性模量的核心要素为颗粒表面间距,因为颗粒表面间距影响了吸附聚合物的压缩程度。增大悬浮液体积分数、减小颗粒粒径均是通过降低颗粒表面间距以及被压缩吸附层的厚度使系统弹性模量上升,表现为弹性变大,最终影响悬浮液的稳定性。
关键词: 陶瓷, 氧化铝, 悬浮液, 流变性能, 弹性模量, 空间稳定
0 引 言
颗粒在介质中的分散与稳定以及悬浮液的流变特性对陶瓷胶态成型工艺具有十分重要的意义。在各种陶瓷制品生产工艺中,绝大多数涉及浆料的制备,例如注浆成型、可塑成型、流延成型、浸渍涂膜等[1-2]。颗粒的分散与稳定是制备高性能陶瓷的基本要求[3]。
悬浮液稳定机制主要包括:静电稳定机制,由介质中带电粒子之间的相互作用产生;聚合物稳定机制,即颗粒间产生的空间位阻作用。稳定剂在颗粒表面的吸附可促进空间稳定,在许多领域得到广泛应用[4]。在聚合物稳定方式中,以 Napper 为代表的研究工作者建立了空间相互作用理论,认为粒子间分散稳定的主要因素是吸附聚合物层间的斥力[5],由于聚合物的存在而产生斥力位能[6]。聚合物以适当的厚度和密度吸附在粒子表面,形成空间稳定层,防止吸力位能占主导地位。影响聚合物稳定的主要因素包括颗粒体积分数、颗粒粒径、聚合物含量等,然而这些特征参数对颗粒间相互作用的影响是未知的。另外,悬浮稳定反映了力的相互作用,现有理论及研究成果缺少对悬浮体系弹性作用及弹性参数的表征,以及弹性影响因素的分析,因此关于弹性作用的研究成为悬浮稳定研究的科学技术难题。
目前对于悬浮液的表征,最佳的方式是流变性能测试,因为流变性能对稳定性条件的任何变化都非常敏感[7],如分散剂类型和浓度、pH 值、其他电解质和添加剂、混合条件、颗粒大小分布和形状、体积分数等[8-9]。动态流变行为是指材料在正弦波规律的应变或应力作用下的力学响应,通过动态流变测试可同时获得材料黏性和弹性行为的信息[10]。在小应变或应力条件下,动态流变测试过程不会对材料本身结构造成影响和破坏,保证了悬浮液中聚合物对颗粒的吸附状态。因此,通过动态流变测试可以有效表征陶瓷颗粒的分散状态,常采用的方法包括应力、应变振幅扫描。Setz 等[11] 研究了 α-Al2O3 悬浮浆料动态流变特性,随着固含量增加,粒子之间的距离越近,吸引和斥力越活跃,产生显著的黏弹性响应。
本文以 Al2O3 悬浮液为研究对象,以聚乙烯醇(PVA)为添加剂,通过流变性能测试,描述了 Al2O3 悬浮液流变特性、结构和稳定性之间的关系。本文的主要目的是探讨影响聚合物空间稳定性的主要因素,以及影响悬浮体系弹性的核心要素。
1 实 验
1. 1 原材料
采用 Al2O3 微粉( 中国蚌埠凯旋电子材料有限公司) 作为原料,颗粒呈球形,用激光粒度分析仪(Bettersize 2000)测得平均直径为 2. 4 μm。采用 PVA 1799(上海阿拉丁生化技术有限公司)作为添加剂。
1. 2 悬浮液制备
先将一定量的 PVA 溶于适量的水中,在 80 ℃ 环境下搅拌、加热至完全溶解,制得质量分数为 12% 的PVA 溶液。随后,将 Al2O3 按照颗粒体积分数 17% ~ 23% 缓慢加入去离子水中,超声分散 10 min。将悬浮液与少量消泡剂混合,以氧化锆球作为研磨介质,在行星球磨机(QM-3SP2,南京大学仪器厂)中以 300 r/min的速度球磨 2 h,得到 Al2O3 与 PVA 的混合悬浮液。
1. 3 流变性能测试
试验采用旋转流变仪 HAAKE MARS 40,测量转子为 P35 / Ti,间隙为 1. 000 mm,温度由 Mars 温度模块控制。试验在连续和振荡剪切两种流变条件下完成,剪切速率从 0 s-1到 200 s-1变化,得到连续流动条件下的流动曲线,同时取对数数据,以确保在较低的剪切速率下有更多的数据点,在振荡剪切条件下测试了悬浮液的黏弹性。为了确定线性黏弹性区域,在恒定频率(1 Hz)下,在应变范围 0. 001 ~ 10 进行了应变扫描试验,并且得到线性黏弹性区域的储能模量 G′。
2 结果与讨论
2. 1 PVA 水溶液的流变分析
图 1 为质量分数 12% 的 PVA 水溶液在不同温度下剪切应力、黏度与剪切速率关系。在低剪切速率下黏度快速降低,反映了 PVA 水溶液存在屈服现象。屈服是聚合物剪切变形的典型特征,这与 PVA 分子三维链状缠绕结构有关系[12],也说明 PVA 水溶液在一定形变范围内存在弹性。PVA 水溶液在 25 ℃ 为典型的宾汉型流体,剪切黏度为 0. 3 Pa·s。随着温度降低,黏度升高,意味着需要更大的剪切应力来产生层间滑移以致黏性流动。PVA 水溶液在 2 ~ 10 ℃表现为剪切变稀现象,呈假塑性流体特性,说明在 200 s-1的剪切速率范围内 PVA 链状分子的解缠绕持续进行;并且温度越低时,在低剪切速率下黏度降低更多。这意味着温度越低,PVA 链状分子的缠绕更加紧密,因而弹性作用越强。
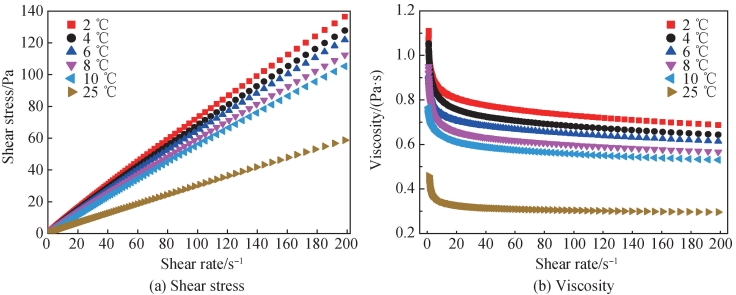
图 1 质量分数 12% 的 PVA 水溶液在不同温度下剪切应力、黏度与剪切速率关系
为了定量表征 PVA 水溶液的弹性,采取了动态流变的振荡模式应变扫描,试验控制振荡频率 1 Hz。图 2 显示了质量分数 12% 的 PVA 水溶液在不同温度下储能模量 G′与剪切应变的双对数关系。在低应变下,观察到一个恒定响应区(平台区域),表明一个未改变的结构。在这个线性区域,PVA 链状网络是稳定的,类似于弹簧,这定义了弹性域[13]。继续增大应变,可以观察到 G′的减小,所施加的应力和应变逐渐让网络结构破坏和解缠绕,弹性逐渐减弱直至消失,并诱导至黏性域的转变。储能模量 G′反映了 PVA 水溶液的弹性大小,由图 2 可知,在给定的试验温度范围内,应变在 1 以下时存在线性黏弹性区域,储能模量 G′为0. 9 ~ 3. 0 Pa。振荡测试反映了 PVA 水溶液在小应变范围内存在弹性,并且温度越低,弹性越大。
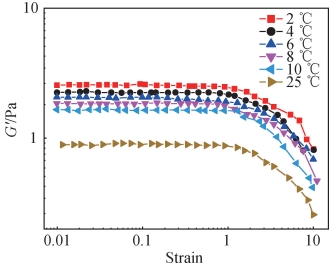
图 2 质量分数 12% 的 PVA 水溶液在不同温度下储能模量与剪切应变的双对数关系
图 3 显示了不同质量分数 PVA 水溶液在10 ℃下储能模量 G′与剪切应变的双对数关系。PVA 质量分数在 12% 、10% 、8% 时的储能模量 G′分别为 1. 60、0. 56、0. 17 Pa,该试验说明增加 PVA 的浓度促进了 PVA 链状分子的缠绕,使弹性增强。
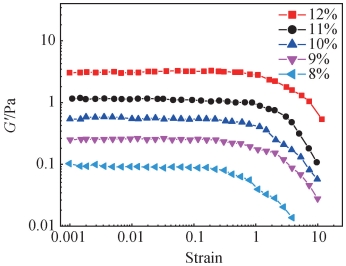
图 3 不同质量分数 PVA 水溶液在 10 ℃下储能模量与剪切应变的双对数关系
2. 2 氧化铝与 PVA 混合悬浮液的稳态流变分析
悬浮液的流变行为比纯液体复杂,因为此时有固体粒子填充,不但聚合物本身存在相互作用力,聚合物与颗粒、颗粒与颗粒同样存在作用力。不同温度下体积分数 20% 、23% 的 Al2O3 悬浮液的黏度与剪切速率关系如图 4 所示,此时 PVA 质量分数均为 4% 。随着剪切速率的增大,整体都是剪切变稀的,但是黏度曲线较纯 PVA 水溶液发生明显变化,在低剪切速率范围内出现了转折突变点。为了更详细分析 Al2O3 悬浮液在剪切过程中的变化,本研究将黏度曲线划分为三个阶段。
第一阶段为黏度快速降低区。这与 PVA 水溶液性质保持一致,同样存在屈服现象,表明了悬浮液在剪切初期呈现出弹性特征。Al2O3 悬浮液的剪切模型如图 5 所示。Al2O3 悬浮液体系可以认为由颗粒、添加剂、溶剂组成的一个框架系统,Al2O3 颗粒与 PVA 由氢键结合,此时 PVA 被压缩在 Al2O3 颗粒间隙中,颗粒与颗粒间由 PVA 阻隔,如图 5(a)所示。当施加剪切应力 τ 后,颗粒在剪切方向上距离增大,原本受到压缩的 PVA 分子链变得松弛,弹性快速释放,如图 5(c)所示,导致黏度快速降低。这一部分黏度降低与受 PVA的压缩程度有关,对比图 4 中两组试验数据,在该区间,体积分数 23% 的悬浮液黏度快速降低了约 1 Pa·s,而体积分数 20% 的悬浮液黏度则降低了约 0. 5 Pa·s,表示体积分数 23% 的悬浮液所含颗粒对 PVA 的压缩更显著,因而剪切扰动后释放愈多。
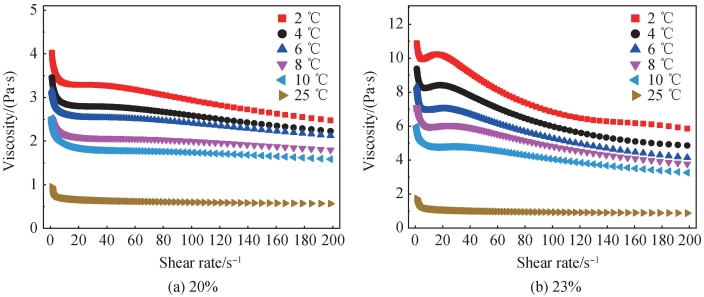
图 4 不同温度下体积分数 20% 、23% 的 Al2O3 悬浮液的黏度与剪切速率关系
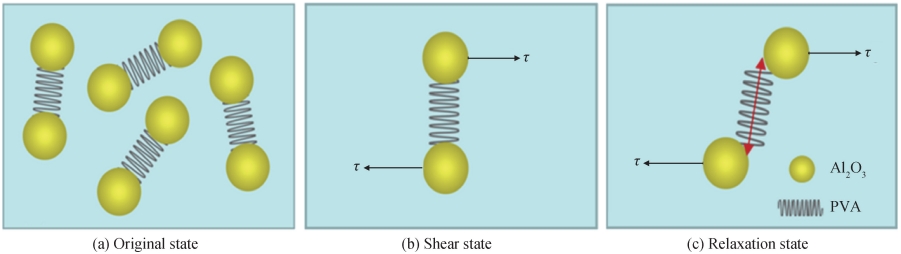
图 5 Al2O3 悬浮液的剪切模型
第二阶段为黏度上升/ 平缓区。当受到压缩的 PVA 分子链弹性释放后,继续施加剪切力,PVA 将存在抵抗外界作用力而出现回拉的趋势,阻碍剪切拉伸,所以黏度会增大,即剪切增稠现象。黏度增大的程度同样与体积分数及温度相关,体积分数 23% 的悬浮液剪切增稠趋势高于体积分数 20% 的悬浮液,这依然与 PVA分子链受压缩状态有关。另外温度越低,弹性越强,反映在图中为黏度上升明显;温度越高,则 PVA 弹性越弱,拉伸效应减弱。在不同温度下纯 PVA 水溶液的流变性能研究中已有阐述和解释(见 2. 1 节)。
第三阶段为黏度继续降低区。随着剪切速率逐渐增大,此时剪切应力大于 PVA 回弹的力学限度,PVA分子继续解缠绕,黏度持续降低,继续保持假塑性流体的特征。
2. 3 氧化铝填充 PVA 水溶液的动态流变分析
研究[14]表明,悬浮液的分散稳定受颗粒间的各种稳定作用机制如静电排斥作用、空间稳定作用以及这些作用的组合的影响。 总位能 U = UR + UA + URE,其中 UR 为静电斥力位能,UA为吸力位能,URE 为弹性斥力位能。对于 Al2O3 填充 PVA 悬浮液体系,弹性斥力位能为稳定的主要因素[15],Karl[16] 提出,围绕粒子的保护层可以被认为类似于交联网络结构,这些吸附层的机械性能决定了粒子的保护作用。如果吸附层弹性模量足够大,在动力学沉降过程中的变形会阻止范德华吸力发挥作用。Karl 推导出压缩聚合物吸附层的弹性斥力位能:
URE = 0. 75Gx5/2(R + δ)1/2 (1)
式中:G 为吸附层的弹性模量;R 为球形颗粒的半径;δ 为吸附聚合物的厚度;x 为被压缩吸附层的厚度。在本研究中,通过动态流变振荡剪切方法对弹性模量精确地定量表征,通常把储能模量 G′看作为弹性模量。对于一个稳定的悬浮液体系,弹性斥力位能要与颗粒的重力势能平衡,因此 URE 是与颗粒重力相关的参数。所以式(1)可写成:
kR³= 0. 75G′x5/2(R + δ)1/2 (2)
式中:k 是与重力势能相关的常数,由于吸附聚合物的厚度 δ 远小于颗粒半径 R,所以式(2)可简化为
kR5/2= 0. 75G′x5/2 (3)
通过式(2)、(3)确定与其中 x、δ、R 因子相关联的体积分数、PVA 含量以及颗粒粒径作为主要因素进行分析研究。
2. 3. 1 体积分数的影响
按照图 6 提出的体积分数改变的系统模型,最初状态的 PVA 为自由状态。当体积分数增大时,相当于颗粒数量增多,相邻颗粒表面间距由 D 减小至 D′,此时 PVA 只能被压缩才能实现更多的颗粒填充。PVA 受到压缩后由于自身的弹性恢复作用,会对颗粒进行排斥,使颗粒不能进一步靠近,从而实现空间位阻稳定。体积分数 17% ~ 26% 的悬浮液储能模量-剪切应变双对数关系如图 7 所示,可以看出应变在 0 ~ 0. 05 时为线性黏弹性区域,即在此应变范围内保持弹性,结构未发生变化。在平台区储能模量 G′分别为 1. 0、2. 5、7. 5、28. 0 Pa,储能模量 G′急剧增大,即弹性更大。因此不难解释在一定体积分数范围内,增大体积分数有益于提高陶瓷悬浮液的稳定性。
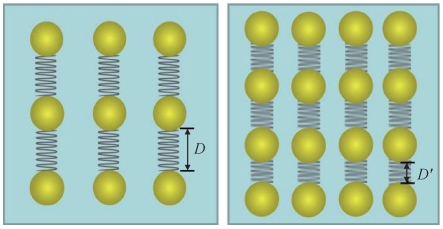
图 6 体积分数改变的系统模型
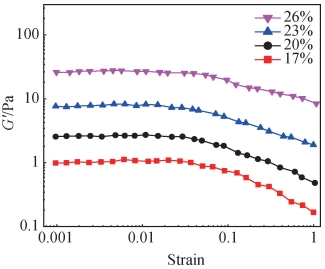
图 7 不同体积分数的 Al2O3 悬浮液储能模量与剪切应变的双对数关系
将 Al2O3 颗粒视为等径小球,并且相邻颗粒间距相同,通过计算得到 17% 、20% 、23% 、26% 四种体积分数所对应的颗粒表面间距 D,分别为 1. 10、0. 91、0. 76、0. 63 μm。对于等径的 Al2O3 颗粒,在式(3)中颗粒半径 R 为定值,因此储能模量 G′与 x5/2成反比。x 值越小,代表了吸附 PVA 层压缩越紧密。通过图 8 中被压缩吸附层的厚度 x 及储能模量 G′与颗粒表面间距 D 的相互关系可以确定体积分数影响陶瓷悬浮液体系稳定性的机制,即随着体积分数增大,颗粒表面间距 D 减小,PVA 被压缩,被压缩吸附层的厚度 x 也减小,通过式(3)最终导致储能模量 G′的增大。
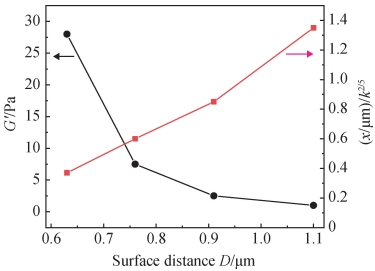
图 8 被压缩吸附层的厚度及储能模量与颗粒表面距离的关系
2. 3. 2 PVA 含量的影响
Al2O3 体积分数为 23% ,PVA 质量分数分别为 3. 5% 、4. 0% 、4. 5% 的悬浮液的储能模量 G′与剪切应变的双对数关系如图 9 所示。三组试验应变均在 0 ~ 0. 05 存在线性黏弹性区域,并且在平台区储能模量 G′分别约为 4. 5、7. 5、10. 5 Pa,呈线性增大规律。对此分析为:体积分数与粒径均不变时,虽然颗粒表面间距不变,但当 PVA 含量较低时,储能模量 G′低,这意味着聚合物链在悬浮液中没有明显的重叠或相互渗透。随着PVA 含量的增加,颗粒间隙中填充了更多的 PVA,此时 PVA 链缠绕更加紧密。这时吸附层的 PVA 更容易被压缩,被压缩吸附层的厚度 x 降低,储能模量 G′上升,导致弹性增加。因此在一定范围内增加聚合物含量能提高系统的弹性,对陶瓷颗粒支撑增强,将有助于提高陶瓷悬浮液的稳定性。
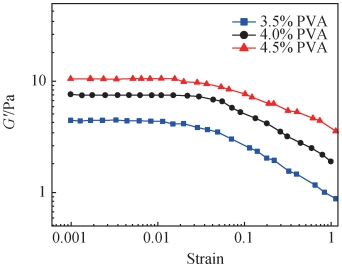
图 9 不同 PVA 质量分数的 Al2O3 悬浮液储能模量与剪切应变的双对数关系
2. 3. 3 颗粒粒径的影响
Al2O3 体积分数为 23% 的不同颗粒粒径的悬浮液储能模量 G′与剪切应变的双对数关系如图 10 所示。颗粒粒径为 0. 1、0. 6、1. 0、2. 4、5. 0 μm 时所对应的悬浮液储能模量 G′分别约为 568. 0、105. 0、44. 6、7. 5、1. 5 Pa。对此分析为:当体积分数、PVA 含量保持不变时,连续相 PVA 的体积和链长尺寸不变。但是实际上粒径减小,粒子数量增多,导致颗粒表面间距缩小。通过计算得到五种颗粒粒径所对应的颗粒表面间距 D,分别为 0. 03、0. 19、0. 31、0. 76、1. 58 μm。
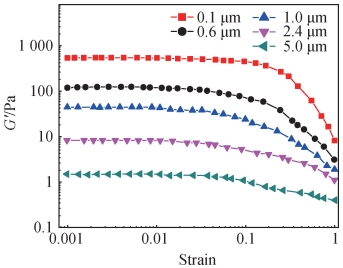
图 10 不同颗粒粒径的 Al2O3 悬浮液储能模量与剪切应变的双对数关系
图 11 为被压缩吸附层的厚度 x 及储能模量 G′与不同粒径颗粒表面间距 D 的关系,粒径的降低使颗粒表面间距 D 减小,被压缩吸附层的厚度 x 进一步变小,通过式(3)可知系统的储能模量 G′快速增大,表现为弹性更强。然而,吸附层 PVA 受压缩程度有限,当达到一定范围时,则出现耗尽絮凝[17]。如图 11 所示,在低颗粒表面间距 D 时,被压缩吸附层的厚度 x 变化缓慢,必然会达到某一极限值后不再降低,此时 PVA 难以进入到颗粒间隙实现压缩。因此,在实际应用中可降低 PVA 的添加量,或降低聚合物的分子量,改变分子链长来实现分散与稳定。
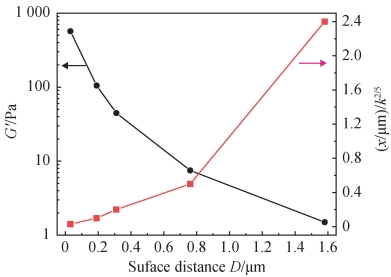
图 11 被压缩吸附层的厚度及储能模量与不同粒径颗粒表面距离的关系
通过以上分析,对于不同粒径、不同体积分数的陶瓷悬浮液体系,可以根据颗粒表面间距大小来合理确定添加剂的选择和使用量问题,以达到系统最佳悬浮稳定状态。
3 结 论
1)纯 PVA 水溶液的流变模型为典型的宾汉模型及假塑性模型,当氧化铝填充后流变曲线发生变化,根据黏度的变化将黏度曲线划分了三个阶段。 产生突变点的原因主要在于 PVA 的弹性特征,增加氧化铝体积分数及降低温度时更明显,表明系统弹性更强。
2)通过振荡应变扫描确定了线性黏弹性区域,并分析了不同因素对储能模量的影响。随着氧化铝体积分数及 PVA 含量增大、颗粒粒径减小,系统储能模量会上升,表现出更强的弹性。
3)对于氧化铝悬浮液,空间稳定的核心要素为颗粒表面间距。氧化铝体积分数、颗粒粒径均是通过改变颗粒表面间距,进而改变被压缩吸附层 PVA 的厚度,最终影响到系统的弹性模量。
参考文献
[1] MORENO R. Colloidal processing of ceramics and composites[J]. Advances in Applied Ceramics, 2012, 111(5/6): 246-253.
[2] ANTUNES F C, GOULART C A, ANDREETA M R B, et al. YSZ/Al2O3 multilayer thick films deposited by spin coating using ceramic suspensions on Al2O3 polycrystalline substrate[J]. Materials Science and Engineering: B, 2018, 228: 60-66.
[3] MORENO R. Better ceramics through colloid chemistry[J]. Journal of the European Ceramic Society, 2020, 40(3): 559-587.
[4] LAZZARI S, MOSCATELLI D, CODARI F, et al. Colloidal stability of polymeric nanoparticles in biological fluids[J]. Journal of Nanoparticle Research, 2012, 14(6): 920.
[5] NAPPER D H. Polymeric stabilization of colloidal dispersions[M]. London: Academic Press, 1983.
[6] CHAKRABORTY S, PANIGRAHI P K. Stability of nanofluid: a review[J]. Applied Thermal Engineering, 2020, 174: 115259.
[7] JIANG T Y, ZUKOSKI C F. Role of particle size and polymer length in rheology of colloid-polymer composites[J]. Macromolecules, 2012, 45(24): 9791-9803.
[8] SINGH B P, MENCHAVEZ R, TAKAI C K, et al. Stability of dispersions of colloidal alumina particles in aqueous suspensions[J]. Journal of Colloid and Interface Science, 2005, 291(1): 181-186.
[9] YAGHTIN M, YAGHTIN A, TANG Z L, et al. Improving the rheological and stability characteristics of highly concentrated aqueous yttria stabilized zirconia slurries[J]. Ceramics International, 2020, 46(17): 26991-26999.
[10] DUDUKOVIC N A, WONG L L, NGUYEN D T, et al. Predicting nanoparticle suspension viscoelasticity for multimaterial 3D printing of silica-titania glass[J]. ACS Applied Nano Materials, 2018, 1(8): 4038-4044.
[11] SETZ L F G, SILVA A C, SANTOS S C, et al. A viscoelastic approach from α-Al2O3 suspensions with high solids content[J]. Journal of the European Ceramic Society, 2013, 33(15/16): 3211-3219.
[12] GUPTA D, JASSAL M, AGRAWAL A K. Atypical rheology and spinning behavior of poly(vinyl alcohol) in a nonaqueous solvent[J]. Polymer Journal, 2019, 51(9): 883-894.
[13] TADROS T. Viscoelastic properties of sterically stabilised emulsions and their stability[J]. Advances in Colloid and Interface Science, 2015, 222: 692-708.
[14] CACUA K, ORDOÑEZ F, ZAPATA C, et al. Surfactant concentration and pH effects on the zeta potential values of alumina nanofluids to inspect stability[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2019, 583: 123960.
[15] HNATKOVA E, HAUSNEROVA B, FILIP P. Evaluation of powder loading and flow properties of Al2O3 ceramic injection molding feedstocks treated with stearic acid[J]. Ceramics International, 2019, 45(16): 20084-20090.
[16] KARL J. Über die funktionen des schutzkolloids[J]. Kolloid-Zeitschrift und Zeitschrift für Polymere, 1964, 197(1): 143-151.
[17] SOUZA S F, MARIANO M, DE FARIAS M A, et al. Effect of depletion forces on the morphological structure of carboxymethyl cellulose and micro/nano cellulose fiber suspensions[J]. Journal of Colloid and Interface Science, 2019, 538: 228-236.
声明:本文由 CERADIR 先进陶瓷在线平台的入驻企业/个人提供或自网络获取,文章内容仅代表作者本人,不代表本网站及 CERADIR 立场,本站不对文章内容真实性、准确性等负责,尤其不对文中产品有关功能性、效果等提供担保。本站提醒读者,文章仅供学习参考,不构成任何投资及应用建议。如需转载,请联系原作者。如涉及作品内容、版权和其它问题,请与我们联系,我们将在第一时间处理!本站拥有对此声明的最终解释权。